• "independent samples t-test" is usually adopted to compare means (1 variable, e.g. age or GPA score) between two groups on a categorical variable in a survey
• if each respondent (i.e. each case) has 2 different scores (i.e. 2 variables) to compare, e.g. GPA of term 1 and GPA of term 2, " Paired Samples T-Test" should be used
• it is used when 2 measures relate to one another
  

• the categorical variable can invovle 2 or more categories
  
• however, T-Test can only compare 2 groups each time
• define which 2 groups will be included in the comparison by pressing the Define Groups button
• when there are only 2 categories in the variable, it is still necessary to define groups
  

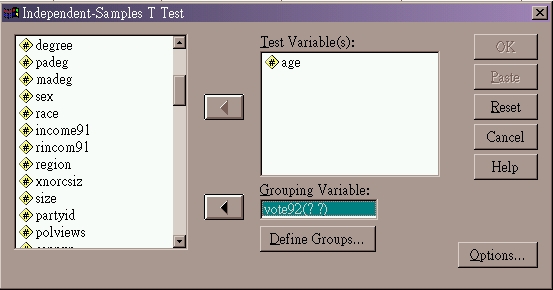
• fill in the codes representing the 2 groups to be compared
• then  press Continue
• as in other analyses, press OK if you want to get the results immediately, or 
• press Paste to copy out the command syntax, then run it in the Syntax window to get the output

• SPSS will first produce the following table to show the mean age of the 2 groups in comparison
• in average, those who voted were about 5 years (47.85 - 42.71) older than those who did not
• from the sample means, we can draw an initial conclusion that voters were older than non-voters
• however, we are interested more in inferring the sample finding to the target population, the above conclusion must be tested for statistical significance
  

T-Test

• the null hypothesis is: voters and non-voters had no difference in age
• 2 rows contain the same nature of informtion: t, df, Sig. (2-tailed) ...
• Equal variances assumed
• Equal variances not assumed
• as you may notice, we have to choose one row of information to believe , but which one?
• Equal variances assumed or Equal variances not assumed?
• variances here refer to the variance of each group mean
• rule of decision:
• the null hypothesis is: the variances of the means (2 groups) are equal
• looking at the pink box, the significance corresponds to the F-value (in green box)
• if the significance level is greater than 0.05, the null hypothesis is accepted
• i.e., choose the blue box Equal variances assumed for information on t-test
• if the significance level is less than or equal to 0.05, the null hypothesis is rejected
• i.e., choose the yellow box Equal variances not assumed for information on t-test
• the significance level is 0.202, therefore null hypothesis is accepted
• we have to choose the blue box Equal variances assumed for information on t-test
  
• the Sig. (2-tailed) tells us about the level of significance of the t-value
• the significance shows .000, but it does not mean the probability is zero, it actually means the significance level is less than 0.0005
• as a convention, we reject the null hypothesis at p  0.05
• hence, we may conclude that voters were older than non-voters in our target population